5. Multilayer Perceptron¶
5.1. Sigmoid function¶
BP algorithm is mainly due to the emergence of Sigmoid function, instead of the previous threshold function to construct neurons.
The Sigmoid function is a monotonically increasing nonlinear function. When the threshold value is large enough, the threshold function can be approximated.
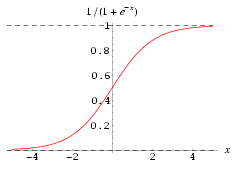
The Sigmoid function is usually written in the following form:
The value range is \((-1,1)\), which can be used instead of the neuron step function:
Due to the complexity of the network structure, the Sigmoid function is used as the transfer function of the neuron. This is the basic idea of multilayer perceptron backpropagation algorithm.
5.2. Back Propagation¶
Back Propagation (BP) algorithm is the optimization of the network through the iterative weights makes the actual mapping relationship between input and output and the desired mapping, descent algorithm by adjusting the layer weights for the objective function to minimize the gradient. The sum of the squared error between the predicted output and the expected output of the network on one or all training samples:
The error of each unit is calculated by layer by layer error of output layer:
Back Propagation Net (BPN) is a kind of multilayer network which is trained by weight of nonlinear differentiable function. BP network is mainly used for:
- function approximation and prediction analysis: using the input vector and the corresponding output vector to train a network to approximate a function or to predict the unknown information;
- pattern recognition: using a specific output vector to associate it with the input vector;
- classification: the input vector is defined in the appropriate manner;
- data compression: reduce the output vector dimension to facilitate transmission and storage.
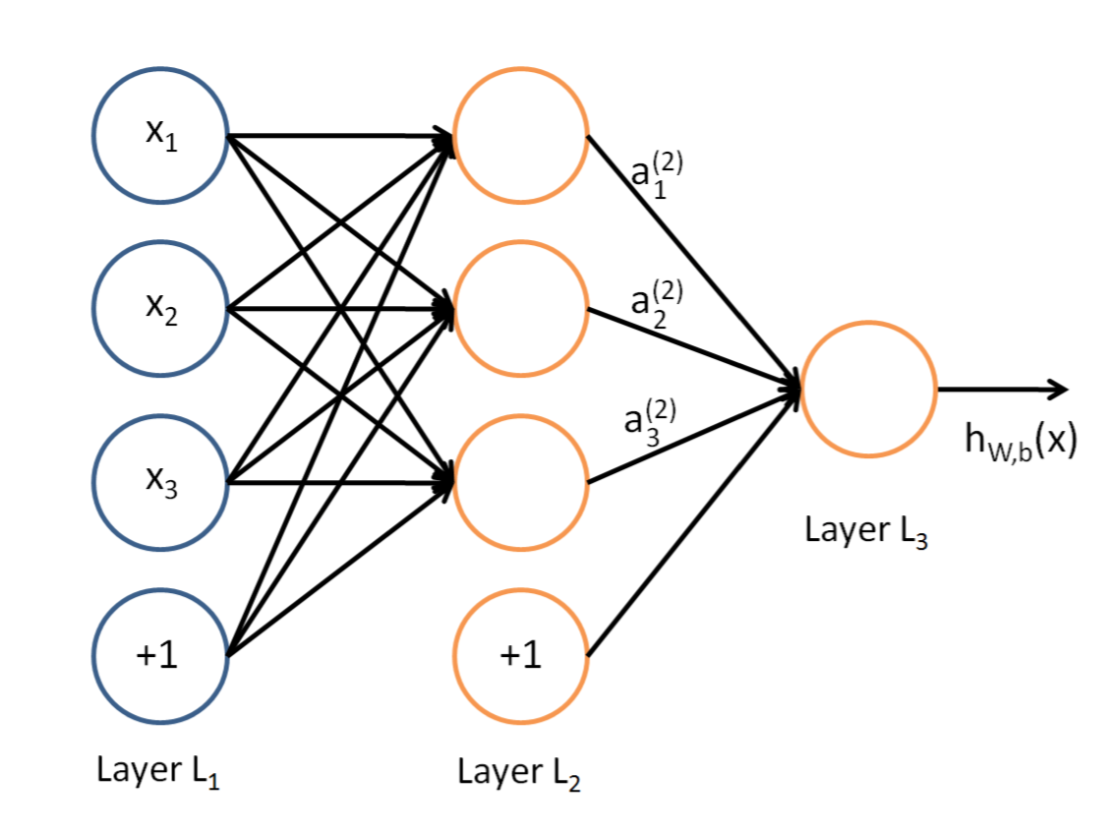
For example, a three tier BP structure is as follows:
It consists of three layers: input layer, hidden layer and output layer. The unit of each layer
is connected with all the units of the adjacent layer, and there is no connection between the units in the
same layer. When a pair of learning samples are provided to the network, the activation value of the neuron
is transmitted from the input layer to the output layer through the intermediate layers, and the input
response of the network is obtained by the neurons in the output layer. Next, according to the direction
of reducing the output of the target and the direction of the actual error, the weights of each link are
modified from the output layer to the input layer.
5.3. Example¶
Suppose you have such a network layer:
- The first layer is the input layer, two neurons containing \(i_1, i_2, b_1\) and intercept;
- The second layer is the hidden layer, including two neurons \(h_1, h_2\) and intercept b2;
- The third layer is the output of \(o_1, o_2\) and \(w_i\) are each line superscript connection weights between layers, we default to the activation function sigmoid function.
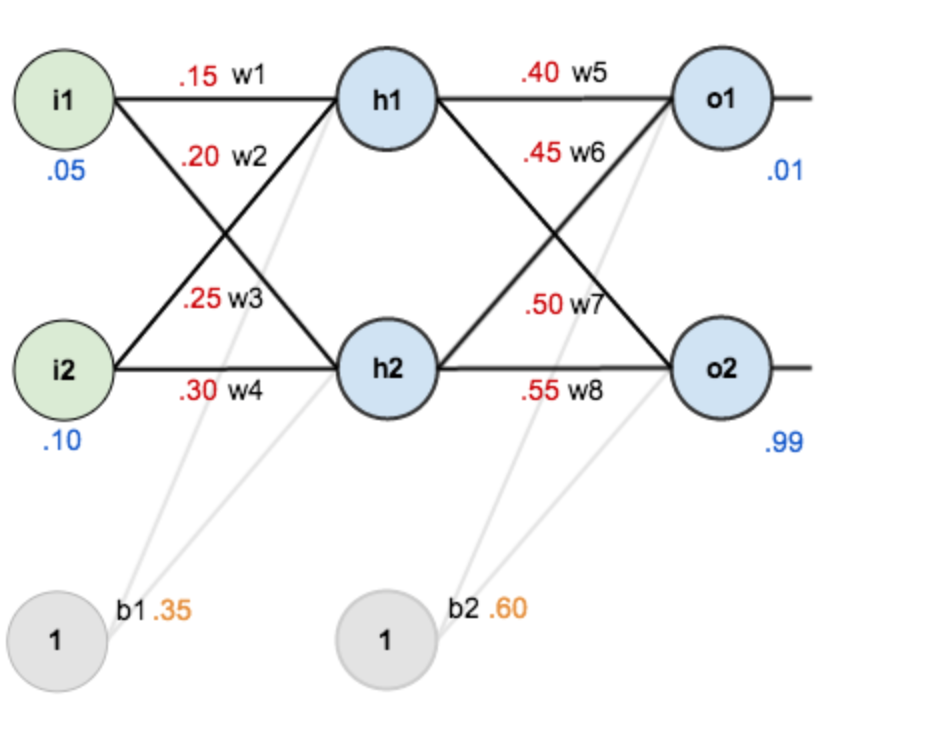
Now give them the initial value, as shown below:
Among them,
- Input data: \(i_1=0.05, i_2=0.10\);
- Output data: \(o_1=0.01, o_2=0.99\);
- Initial weight: \(w_1=0.15, w_2=0.20, w_3=0.25, w_4=0.30, w_5=0.40, w_6=0.45, w_7=0.50, w_8=0.88\);
Objective: to give input data \(i_1, i_2\) (0.05 and 0.10), so that the output is as close as possible to the original output \(o_1, o_2\) (0.01 and 0.99).
5.3.1. Step 1: Forward Propagation¶
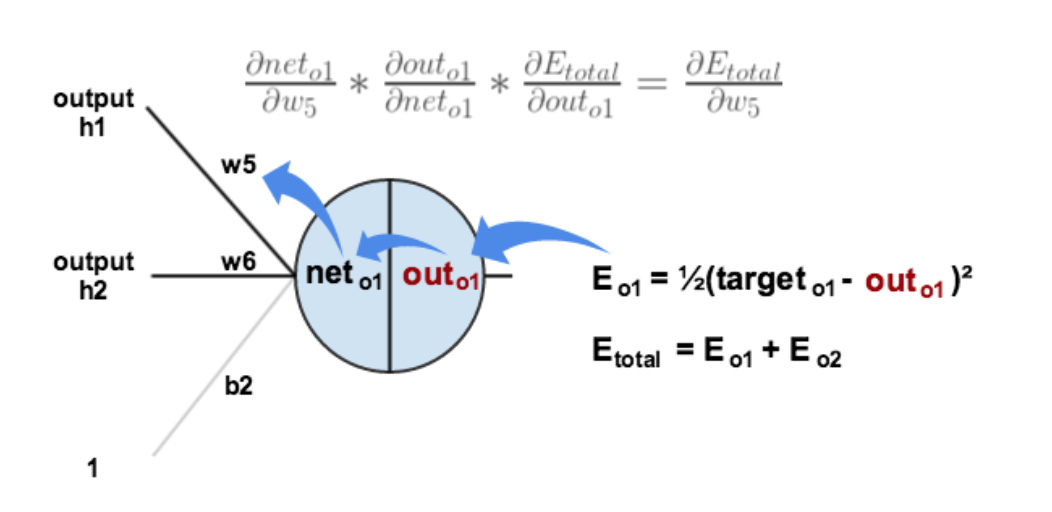
5.3.2. Step 2: Back Propagation¶
5.3.2.1. Calculate the total error¶
Total error (square error):
For example, the target output for \(o_1\) is 0.01 but the neural network output 0.75136507, therefore its error is:
Repeating this process for \(o_2\) (remembering that the target is 0.99) we get:
The total error for the neural network is the sum of these errors:
5.4. Code¶
First, import necessary packages:
import random
import math
Define network:
class NeuralNetwork:
LEARNING_RATE = 0.5
def __init__(self, num_inputs, num_hidden, num_outputs,
hidden_layer_weights=None,
hidden_layer_bias=None,
output_layer_weights=None,
output_layer_bias=None):
self.num_inputs = num_inputs
self.hidden_layer = NeuronLayer(num_hidden, hidden_layer_bias)
self.output_layer = NeuronLayer(num_outputs, output_layer_bias)
self.init_weights_from_inputs_to_hidden_layer_neurons(hidden_layer_weights)
self.init_weights_from_hidden_layer_neurons_to_output_layer_neurons(output_layer_weights)
def init_weights_from_inputs_to_hidden_layer_neurons(self, hidden_layer_weights):
weight_num = 0
for h in range(len(self.hidden_layer.neurons)):
for i in range(self.num_inputs):
if not hidden_layer_weights:
self.hidden_layer.neurons[h].weights.append(random.random())
else:
self.hidden_layer.neurons[h].weights.append(hidden_layer_weights[weight_num])
weight_num += 1
def init_weights_from_hidden_layer_neurons_to_output_layer_neurons(self, output_layer_weights):
weight_num = 0
for o in range(len(self.output_layer.neurons)):
for h in range(len(self.hidden_layer.neurons)):
if not output_layer_weights:
self.output_layer.neurons[o].weights.append(random.random())
else:
self.output_layer.neurons[o].weights.append(output_layer_weights[weight_num])
weight_num += 1
def inspect(self):
print('------')
print('* Inputs: {}'.format(self.num_inputs))
print('------')
print('Hidden Layer')
self.hidden_layer.inspect()
print('------')
print('* Output Layer')
self.output_layer.inspect()
print('------')
def feed_forward(self, inputs):
hidden_layer_outputs = self.hidden_layer.feed_forward(inputs)
return self.output_layer.feed_forward(hidden_layer_outputs)
# Uses online learning, ie updating the weights after each training case
def train(self, training_inputs, training_outputs):
self.feed_forward(training_inputs)
# 1. Output neuron deltas
pd_errors_wrt_output_neuron_total_net_input = [0] * len(self.output_layer.neurons)
for o in range(len(self.output_layer.neurons)):
# ∂E/∂zⱼ
pd_errors_wrt_output_neuron_total_net_input[o] = self.output_layer.neurons[
o].calculate_pd_error_wrt_total_net_input(training_outputs[o])
# 2. Hidden neuron deltas
pd_errors_wrt_hidden_neuron_total_net_input = [0] * len(self.hidden_layer.neurons)
for h in range(len(self.hidden_layer.neurons)):
# We need to calculate the derivative of the error with respect to the output of each hidden layer neuron
# dE/dyⱼ = Σ ∂E/∂zⱼ * ∂z/∂yⱼ = Σ ∂E/∂zⱼ * wᵢⱼ
d_error_wrt_hidden_neuron_output = 0
for o in range(len(self.output_layer.neurons)):
d_error_wrt_hidden_neuron_output += pd_errors_wrt_output_neuron_total_net_input[o] * \
self.output_layer.neurons[o].weights[h]
# ∂E/∂zⱼ = dE/dyⱼ * ∂zⱼ/∂
pd_errors_wrt_hidden_neuron_total_net_input[h] = d_error_wrt_hidden_neuron_output * \
self.hidden_layer.neurons[
h].calculate_pd_total_net_input_wrt_input()
# 3. Update output neuron weights
for o in range(len(self.output_layer.neurons)):
for w_ho in range(len(self.output_layer.neurons[o].weights)):
# ∂Eⱼ/∂wᵢⱼ = ∂E/∂zⱼ * ∂zⱼ/∂wᵢⱼ
pd_error_wrt_weight = pd_errors_wrt_output_neuron_total_net_input[o] * self.output_layer.neurons[
o].calculate_pd_total_net_input_wrt_weight(w_ho)
# Δw = α * ∂Eⱼ/∂wᵢ
self.output_layer.neurons[o].weights[w_ho] -= self.LEARNING_RATE * pd_error_wrt_weight
# 4. Update hidden neuron weights
for h in range(len(self.hidden_layer.neurons)):
for w_ih in range(len(self.hidden_layer.neurons[h].weights)):
# ∂Eⱼ/∂wᵢ = ∂E/∂zⱼ * ∂zⱼ/∂wᵢ
pd_error_wrt_weight = pd_errors_wrt_hidden_neuron_total_net_input[h] * self.hidden_layer.neurons[
h].calculate_pd_total_net_input_wrt_weight(w_ih)
# Δw = α * ∂Eⱼ/∂wᵢ
self.hidden_layer.neurons[h].weights[w_ih] -= self.LEARNING_RATE * pd_error_wrt_weight
def calculate_total_error(self, training_sets):
total_error = 0
for t in range(len(training_sets)):
training_inputs, training_outputs = training_sets[t]
self.feed_forward(training_inputs)
for o in range(len(training_outputs)):
total_error += self.output_layer.neurons[o].calculate_error(training_outputs[o])
return total_error
Define layer:
class NeuronLayer:
def __init__(self, num_neurons, bias):
# Every neuron in a layer shares the same bias
self.bias = bias if bias else random.random()
self.neurons = []
for i in range(num_neurons):
self.neurons.append(Neuron(self.bias))
def inspect(self):
print('Neurons:', len(self.neurons))
for n in range(len(self.neurons)):
print(' Neuron', n)
for w in range(len(self.neurons[n].weights)):
print(' Weight:', self.neurons[n].weights[w])
print(' Bias:', self.bias)
def feed_forward(self, inputs):
outputs = []
for neuron in self.neurons:
outputs.append(neuron.calculate_output(inputs))
return outputs
def get_outputs(self):
outputs = []
for neuron in self.neurons:
outputs.append(neuron.output)
return outputs
Define neuron:
.. literalinclude:: mlp_bp.py
start-after: neuron-start end-before: neuron-end
Put all together, and run example:
nn = NeuralNetwork(2, 2, 2,
hidden_layer_weights=[0.15, 0.2, 0.25, 0.3],
hidden_layer_bias=0.35,
output_layer_weights=[0.4, 0.45, 0.5, 0.55],
output_layer_bias=0.6)
for i in range(10000):
nn.train([0.05, 0.1], [0.01, 0.99])
print(i, round(nn.calculate_total_error([[[0.05, 0.1], [0.01, 0.99]]]), 9))
# XOR example:
# training_sets = [
# [[0, 0], [0]],
# [[0, 1], [1]],
# [[1, 0], [1]],
# [[1, 1], [0]]
# ]
# nn = NeuralNetwork(len(training_sets[0][0]), 5, len(training_sets[0][1]))
# for i in range(10000):
# training_inputs, training_outputs = random.choice(training_sets)
# nn.train(training_inputs, training_outputs)
# print(i, nn.calculate_total_error(training_sets))
Please Enjoy!
| [1] | Wikipedia article on Backpropagation. http://en.wikipedia.org/wiki/Backpropagation#Finding_the_derivative_of_the_error |
| [2] | Neural Networks for Machine Learning course on Coursera by Geoffrey Hinton. https://class.coursera.org/neuralnets-2012-001/lecture/39 |
| [3] | The Back Propagation Algorithm. https://www4.rgu.ac.uk/files/chapter3%20-%20bp.pdf |