6. Convolution Neural Networks¶
6.1. Introduction¶
Convolutional Neural Networks (CNN) are now a standard way of image classification – there are publicly accessible deep learning frameworks, trained models and services. It’s more time consuming to install stuff like caffe [1] than to perform state-of-the-art object classification or detection. We also have many methods of getting knowledge - there is a large number of deep learning courses [2] /MOOCs [3], free e-books [4] or even direct ways of accessing to the strongest Deep/Machine Learning minds such as Yoshua Bengio [5], Andrew NG [6] or Yann Lecun [7] by Quora, Facebook or G+.
Nevertheless, when I wanted to get deeper insight in CNN, I could not find a “CNN backpropagation for dummies”. Notoriously I met with statements like: “If you understand backpropagation in standard neural networks, there should not be a problem with understanding it in CNN” or “All things are nearly the same, except matrix multiplications are replaced by convolutions”. And of course I saw tons of ready equations.
It was a little consoling, when I found out that I am not alone, for example: Hello, when
computing the gradients CNN, the weights need to be rotated, Why ? [8]
The answer on above question, that concerns the need of rotation on weights in gradient computing, will be a result of this long post.
6.2. Back Propagation¶
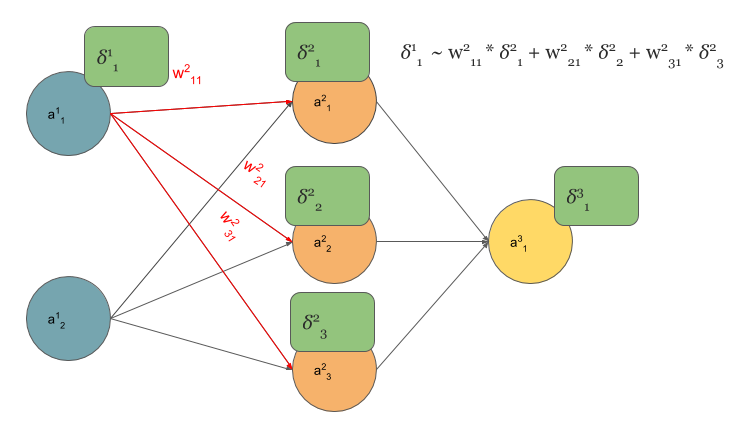
We start from multilayer perceptron and counting delta errors on fingers:
We see on above picture that \(\delta_1^1\) is proportional to deltas from next layer that are scaled by weights.
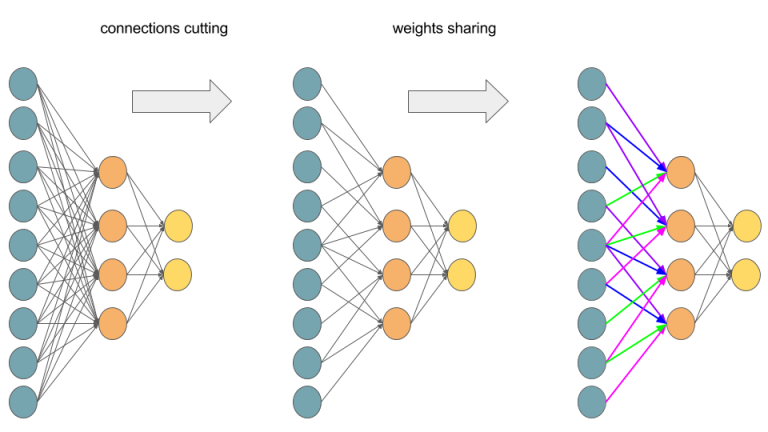
But how do we connect concept of MLP with Convolutional Neural Network? Let’s play with MLP:
If you are not sure that after connections cutting and weights sharing we get one layer Convolutional Neural Network, I hope that below picture will convince you:
The idea behind this figure is to show, that such neural network configuration is identical with a 2D convolution operation and weights are just filters (also called kernels, convolution matrices, or masks).
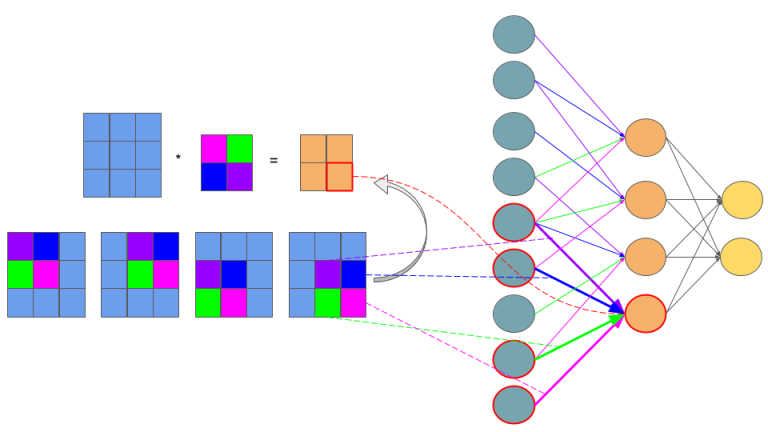
Now we can come back to gradient computing by counting on fingers, but from now we will be only focused on CNN. Let’s begin:
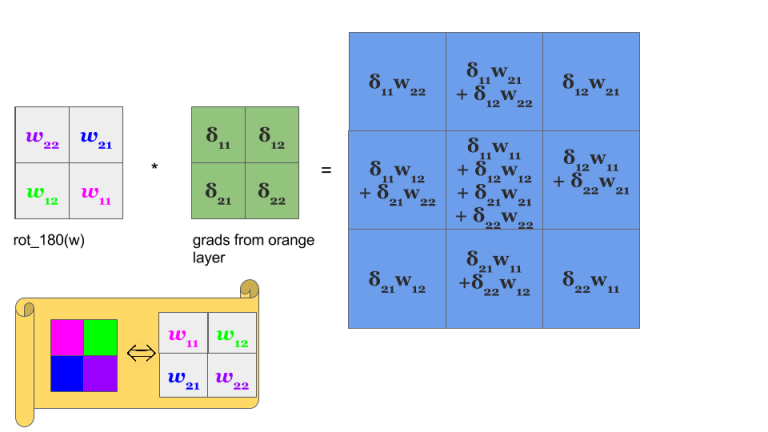
No magic here, we have just summed in “blue layer” scaled by weights gradients from “orange” layer. Same process as in MLP’s backpropagation. However, in the standard approach we talk about dot products and here we have … yup, again convolution:
Yeah, it is a bit different convolution than in previous (forward) case. There we did so called valid convolution, while here we do a full convolution (more about nomenclature here [9] ). What is more, we rotate our kernel by 180 degrees. But still, we are talking about convolution!
Now, I have some good news and some bad news:
- you see (BTW, sorry for pictures aesthetics), that matrix dot products are replaced by convolution operations both in feed forward and backpropagation.
- you know that seeing something and understanding something … yup, we are going now to get our hands dirty and prove above statement before getting next, I recommend to read, mentioned already in the disclaimer, chapter 2 [10] of M. Nielsen book. I tried to make all quantities to be consistent with work of Michael.
In the standard MLP, we can define an error of neuron \(j\) as:
where \(z_j^l\) is just:
and for clarity, \(a_j^l = \sigma(z_j^l)\), where \(\sigma\) is an activation function such as sigmoid, hyperbolic tangent or relu [11].
But here, we do not have MLP but CNN and matrix multiplications are replaced by convolutions as we discussed before. So instead of \(z_j\) we do have a \(z_{x,y}\):
Above equation is just a convolution operation during feedforward phase illustrated in the above picture titled ‘Feedforward in CNN is identical with convolution operation’[12]
Now we can get to the point and answer the question Hello, when computing the gradients CNN,
the weights need to be rotated, Why ? [8]
We start from statement:
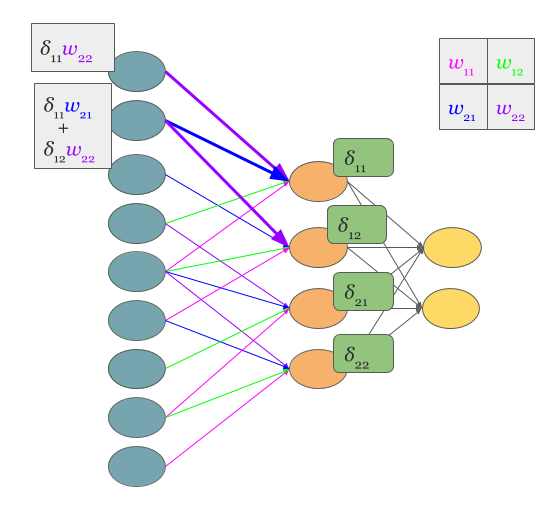
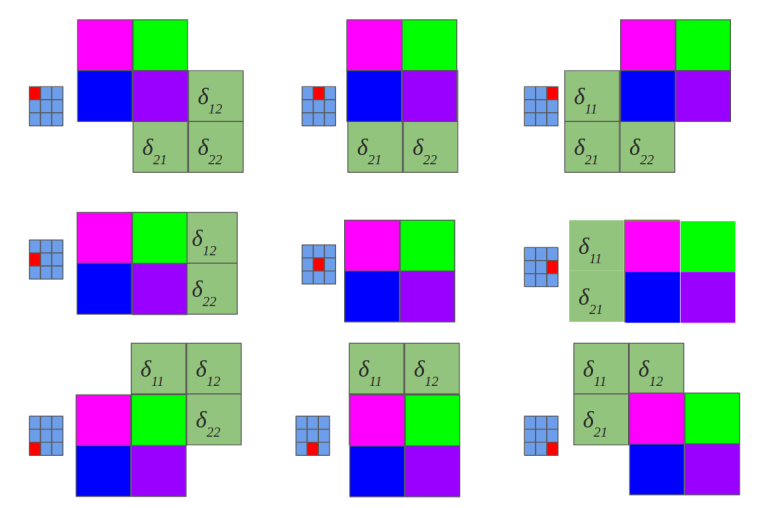
We know that \(z_{x,y}^l\) is in relation to \(z_{x',y'}^{l+1}\) which is indirectly showed in the above picture titled ‘Backpropagation also results with convolution’. So sums are the result of chain rule. Let’s move on:
First term is replaced by definition of error, while second has become large because we put it here expression on \(z_{x',y'}^{l+1}\). However, we do not have to fear of this big monster – all components of sums equal 0, except these ones that are indexed: \(x=x'-a\) and \(y=y'-b\). So:
If “math;`x=x’-a` and \(y=y'-b\) then it is obvious that \(a=x'-x\) and \(b=y'-y\) so we can reformulate above equation to:
OK, our last equation is just …
Where is the rotation of weights? Actually \(ROT180(w_{x,y}^{l+1}) = w_{-x, -y}^{l+1}\).
So the answer on question Hello, when computing the gradients CNN, the weights need to be rotated,
Why ? [8] is simple: the rotation of the weights just results from derivation of delta error in
Convolution Neural Network.
OK, we are really close to the end. One more ingredient of backpropagation algorithm is update of weights \(\frac{\partial C}{\partial w_{a,b}^l}\):
So paraphrasing the backpropagation algorithm [13] for CNN:
- Input \(x\): set the corresponding activation \(a^1\) for the input layer.
- Feedforward: for each \(l = 2,3, \cdots ,L\), compute \(z_{x,y}^l = w^l * \sigma(z_{x,y}^{l-1}) + b_{x,y}^l\) and \(a_{x,y}^l = \sigma(z_{x,y}^l)\)
- Output error \(\delta^L\): Compute the vector \(\delta^L = \nabla_a C \odot \sigma'(z^L)\)
- Backpropagate the error: For each \(l=L-1,L-2,\cdots ,2\), compute \(\delta_{x,y}^l =\delta^{l+1} * ROT180(w_{x,y}^{l+1}) \sigma'(z_{x,y}^l)\)
- Output: The gradient of the cost function is given by \(\frac{\partial C}{\partial w_{a,b}^l} =\delta_{a,b}^l * \sigma(ROT180(z_{a,b}^{l-1}))\)
6.3. Visualizing Features¶
It’s been shown many times that convolutional neural nets are very good at recognizing patterns in order to classify images. But what patterns are they actually looking for?
I attempted to recreate the techniques described in [14] to project features in the convnet back to pixel space.
In order to do this, we first need to define and train a convolutional network. Due to lack of training power, I couldn’t train on ImageNet and had to use CIFAR-10, a dataset of \(32x32\) images in 10 classes. The network structure was pretty standard: two convolutional layers, each with \(2x2\) max pooling and a reLu gate, followed by a fully-connected layer and a softmax classifier.
We’re only trying to visualize the features in the convolutional layers, so we can effectively ignore the fully-connected and softmax layers.
Features in a convolutional network are simply numbers that represent how present a certain pattern is. The intuition behind displaying these features is pretty simple: we input one image, and retrieve the matrix of features. We set every feature to 0 except one, and pass it backwards through the network until reaching the pixel layer. The challenge here lies in how to effectively pass data backwards through a convolutional network.
We can approach this problem step-by-step. There are three main portions to a convolutional layer. The actual convolution, some max-pooling, and a nonlinearity (in our case, a rectified linear unit). If we can figure out how to calculate the inputs to these units given their outputs, we can pass any feature back to the pixel input.
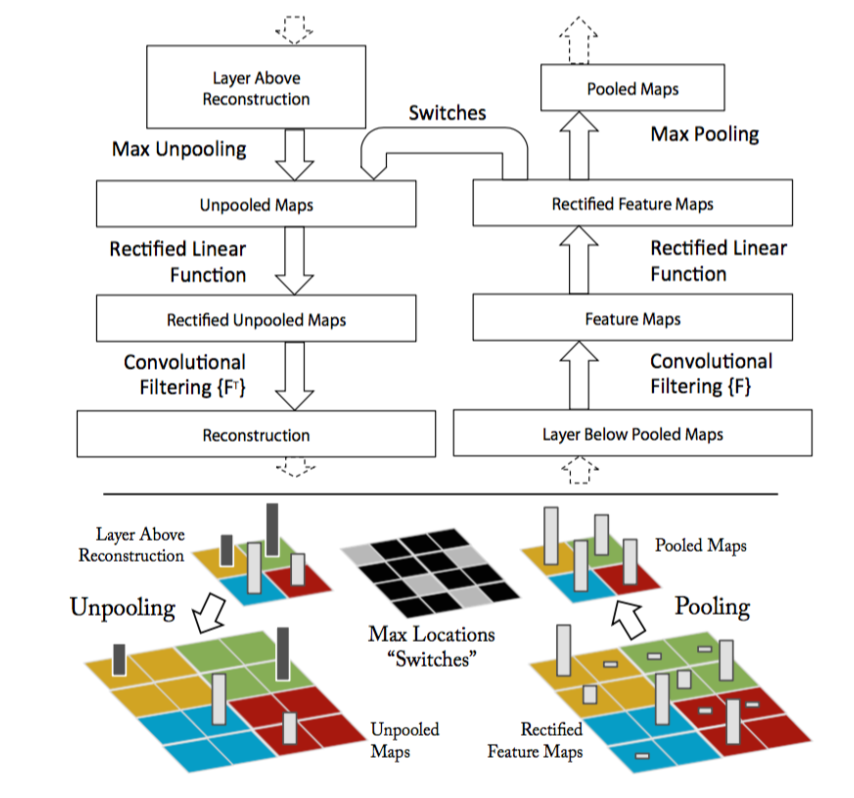
image from [14].
Here, the paper introduces a structure called a deconvolutional layer. However, in practice, this is simply a regular convolutional layer with its filters transposed. By applying these transposed filters to the output of a convolutional layer, the input can be retrieved.
A max-pool gate cannot be reversed on its own, as data about the non-maximum features is lost. The paper describes a method in which the positions of each maximum is recorded and saved during forward propagation, and when features are passed backwards, they are placed where the maximums had originated from. In my recreation, I took an even simpler route and just set the whole \(2x2\) square equal to the maximum activation.
Finally, the rectified linear unit. It’s the easiest one to reverse, we just need to pass the data through a reLu again when moving backwards.
To test these techniques out, I trained a standard convolutional network on CIFAR-10. First, I passed one of the training images, a dog, through the network and recorded the various features.

our favorite dog.
As you can see, there are quite a variety of patterns the network is looking for. You can see evidence of the original dog picture in these feature activations, most prominently the arms.
Now, let’s see how these features change when different images are passed through.
This image shows all the different pixel representations of the activations of feature #7, when a variety of images are used. It’s clear that this feature activates when green is present. You can really see the original picture in this feature, since it probably just captures the overall color green rather than some specific pattern.
Finally, to gain some intuition of how images activated each feature, I passed in a whole batch of images and saved the maximum activations.
Which features were activated by which images? There’s some interesting stuff going on here. Some of the features are activated simply by the presence of a certain color. The green frog and red car probably contained the most of their respective colors in the batch of images.
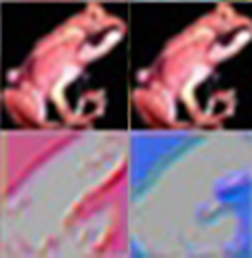
two activations from the above image.
However, here are two features which are activated the most by a red frog image. The feature activations show an outline, but one is in red and the other is in blue. Most likely, this feature isn’t getting activated by the frog itself, but by the black background. Visualizing the features of a convolutional network allows us to see such details.
So, what happens if we go farther, and look at the second convolutional layer?
I took the feature activations for the dog again, this time on the second convolutional layer. Already some differences can be spotted. The presence of the original image here is much harder to see.
It’s a good sign that all the features are activated in different places. Ideally, we want features to have minimal correlation with one another.
Finally, let’s examine how a second layer feature activates when various images are passed in.
For the majority of these images, feature #9 activated at dark locations of the original image. However, there are still outliers to this, so there is probably more to this feature than that.
For most features, it’s a lot harder to tell what part of the image activated it, since second layer features are made of any linear combination of first layer features. I’m sure that if the network was trained on a higher resolution image set, these features would become more apparent.
6.4. Code¶
try:
import tensorflow as tf
import numpy as np
import pickle
from tensorflow.python.platform import gfile
from random import randint
import os
from scipy.misc import imsave
from matplotlib import pyplot as plt
except ImportError:
raise ValueError("Please install tensorflow and matplotlib.")
def unpickle(file):
fo = open(file, 'rb')
dict = pickle.load(fo)
fo.close()
return dict
def initWeight(shape):
weights = tf.truncated_normal(shape, stddev=0.1)
return tf.Variable(weights)
# start with 0.1 so reLu isnt always 0
def initBias(shape):
bias = tf.constant(0.1, shape=shape)
return tf.Variable(bias)
# the convolution with padding of 1 on each side, and moves by 1.
def conv2d(x, W):
return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding="SAME")
# max pooling basically shrinks it by 2x, taking the highest value on each feature.
def maxPool2d(x):
return tf.nn.max_pool(x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding="SAME")
batchsize = 50
imagesize = 32
colors = 3
sess = tf.InteractiveSession()
img = tf.placeholder("float", shape=[None, imagesize, imagesize, colors])
lbl = tf.placeholder("float", shape=[None, 10])
# for each 5x5 area, check for 32 features over 3 color channels
wConv1 = initWeight([5, 5, colors, 32])
bConv1 = initBias([32])
# move the conv filter over the picture
conv1 = conv2d(img, wConv1)
# adds bias
bias1 = conv1 + bConv1
# relu = max(0,x), adds nonlinearality
relu1 = tf.nn.relu(bias1)
# maxpool to 16x16
pool1 = maxPool2d(relu1)
# second conv layer, takes a 16x16 with 32 layers, turns to 8x8 with 64 layers
wConv2 = initWeight([5, 5, 32, 64])
bConv2 = initBias([64])
conv2 = conv2d(pool1, wConv2)
bias2 = conv2 + bConv2
relu2 = tf.nn.relu(bias2)
pool2 = maxPool2d(relu2)
# fully-connected is just a regular neural net: 8*8*64 for each training data
wFc1 = initWeight([(imagesize / 4) * (imagesize / 4) * 64, 1024])
bFc1 = initBias([1024])
# reduce dimensions to flatten
pool2flat = tf.reshape(pool2, [-1, (imagesize / 4) * (imagesize / 4) * 64])
# 128 training set by 2304 data points
fc1 = tf.matmul(pool2flat, wFc1) + bFc1
relu3 = tf.nn.relu(fc1)
# dropout removes duplicate weights
keepProb = tf.placeholder("float")
drop = tf.nn.dropout(relu3, keepProb)
wFc2 = initWeight([1024, 10])
bFc2 = initWeight([10])
# softmax converts individual probabilities to percentages
guesses = tf.nn.softmax(tf.matmul(drop, wFc2) + bFc2)
# how wrong it is
cross_entropy = -tf.reduce_sum(lbl * tf.log(guesses + 1e-9))
# theres a lot of tensorflow optimizers such as gradient descent
# adam is one of them
optimizer = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
# array of bools, checking if each guess was correct
correct_prediction = tf.equal(tf.argmax(guesses, 1), tf.argmax(lbl, 1))
# represent the correctness as a float [1,1,0,1] -> 0.75
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
sess.run(tf.initialize_all_variables())
batch = unpickle("cifar-10-batches-py/data_batch_1")
validationData = batch["data"][555:batchsize + 555]
validationRawLabel = batch["labels"][555:batchsize + 555]
validationLabel = np.zeros((batchsize, 10))
validationLabel[np.arange(batchsize), validationRawLabel] = 1
validationData = validationData / 255.0
validationData = np.reshape(validationData, [-1, 3, 32, 32])
validationData = np.swapaxes(validationData, 1, 3)
saver = tf.train.Saver()
saver.restore(sess, tf.train.latest_checkpoint(os.getcwd() + "/training/"))
# train for 20000
# print mnistbatch[0].shape
def train():
for i in range(20000):
randomint = randint(0, 10000 - batchsize - 1)
trainingData = batch["data"][randomint:batchsize + randomint]
rawlabel = batch["labels"][randomint:batchsize + randomint]
trainingLabel = np.zeros((batchsize, 10))
trainingLabel[np.arange(batchsize), rawlabel] = 1
trainingData = trainingData / 255.0
trainingData = np.reshape(trainingData, [-1, 3, 32, 32])
trainingData = np.swapaxes(trainingData, 1, 3)
if i % 10 == 0:
train_accuracy = accuracy.eval(feed_dict={
img: validationData, lbl: validationLabel, keepProb: 1.0})
print("step %d, training accuracy %g" % (i, train_accuracy))
if i % 50 == 0:
saver.save(sess, os.getcwd() + "/training/train", global_step=i)
optimizer.run(feed_dict={img: trainingData, lbl: trainingLabel, keepProb: 0.5})
print(i)
def unpool(value, name='unpool'):
"""N-dimensional version of the unpooling operation from
https://www.robots.ox.ac.uk/~vgg/rg/papers/Dosovitskiy_Learning_to_Generate_2015_CVPR_paper.pdf
:param value: A Tensor of shape [b, d0, d1, ..., dn, ch]
:return: A Tensor of shape [b, 2*d0, 2*d1, ..., 2*dn, ch]
"""
with tf.name_scope(name) as scope:
sh = value.get_shape().as_list()
dim = len(sh[1:-1])
out = (tf.reshape(value, [-1] + sh[-dim:]))
for i in range(dim, 0, -1):
out = tf.concat(i, [out, out])
out_size = [-1] + [s * 2 for s in sh[1:-1]] + [sh[-1]]
out = tf.reshape(out, out_size, name=scope)
return out
def display():
print("displaying")
batchsizeFeatures = 50
imageIndex = 56
inputImage = batch["data"][imageIndex:imageIndex + batchsizeFeatures]
inputImage = inputImage / 255.0
inputImage = np.reshape(inputImage, [-1, 3, 32, 32])
inputImage = np.swapaxes(inputImage, 1, 3)
inputLabel = np.zeros((batchsize, 10))
inputLabel[np.arange(1), batch["labels"][imageIndex:imageIndex + batchsizeFeatures]] = 1
# inputLabel = batch["labels"][54]
# prints a given image
# saves pixel-representations of features from Conv layer 1
featuresReLu1 = tf.placeholder("float", [None, 32, 32, 32])
unReLu = tf.nn.relu(featuresReLu1)
unBias = unReLu
unConv = tf.nn.conv2d_transpose(unBias, wConv1, output_shape=[batchsizeFeatures, imagesize, imagesize, colors],
strides=[1, 1, 1, 1], padding="SAME")
activations1 = relu1.eval(feed_dict={img: inputImage, lbl: inputLabel, keepProb: 1.0})
print(np.shape(activations1))
# display features
for i in range(32):
isolated = activations1.copy()
isolated[:, :, :, :i] = 0
isolated[:, :, :, i + 1:] = 0
print(np.shape(isolated))
totals = np.sum(isolated, axis=(1, 2, 3))
best = np.argmin(totals, axis=0)
print(best)
pixelactive = unConv.eval(feed_dict={featuresReLu1: isolated})
# totals = np.sum(pixelactive,axis=(1,2,3))
# best = np.argmax(totals,axis=0)
# best = 0
saveImage(pixelactive[best], "activ" + str(i) + ".png")
saveImage(inputImage[best], "activ" + str(i) + "-base.png")
# display same feature for many images
# for i in xrange(batchsizeFeatures):
# isolated = activations1.copy()
# isolated[:,:,:,:6] = 0
# isolated[:,:,:,7:] = 0
# pixelactive = unConv.eval(feed_dict={featuresReLu1: isolated})
# totals = np.sum(pixelactive,axis=(1,2,3))
# best = np.argmax(totals,axis=0)
# saveImage(pixelactive[i],"activ"+str(i)+".png")
# saveImage(inputImage[i],"activ"+str(i)+"-base.png")
# saves pixel-representations of features from Conv layer 2
featuresReLu2 = tf.placeholder("float", [None, 16, 16, 64])
unReLu2 = tf.nn.relu(featuresReLu2)
unBias2 = unReLu2
unConv2 = tf.nn.conv2d_transpose(unBias2, wConv2,
output_shape=[batchsizeFeatures, imagesize / 2, imagesize / 2, 32],
strides=[1, 1, 1, 1], padding="SAME")
unPool = unpool(unConv2)
unReLu = tf.nn.relu(unPool)
unBias = unReLu
unConv = tf.nn.conv2d_transpose(unBias, wConv1, output_shape=[batchsizeFeatures, imagesize, imagesize, colors],
strides=[1, 1, 1, 1], padding="SAME")
activations1 = relu2.eval(feed_dict={img: inputImage, lbl: inputLabel, keepProb: 1.0})
print(np.shape(activations1))
# display features
# for i in xrange(64):
# isolated = activations1.copy()
# isolated[:,:,:,:i] = 0
# isolated[:,:,:,i+1:] = 0
# pixelactive = unConv.eval(feed_dict={featuresReLu2: isolated})
# # totals = np.sum(pixelactive,axis=(1,2,3))
# # best = np.argmax(totals,axis=0)
# best = 0
# saveImage(pixelactive[best],"activ"+str(i)+".png")
# saveImage(inputImage[best],"activ"+str(i)+"-base.png")
# display same feature for many images
# for i in xrange(batchsizeFeatures):
# isolated = activations1.copy()
# isolated[:,:,:,:8] = 0
# isolated[:,:,:,9:] = 0
# pixelactive = unConv.eval(feed_dict={featuresReLu2: isolated})
# totals = np.sum(pixelactive,axis=(1,2,3))
# # best = np.argmax(totals,axis=0)
# # best = 0
# saveImage(pixelactive[i],"activ"+str(i)+".png")
# saveImage(inputImage[i],"activ"+str(i)+"-base.png")
def saveImage(inputImage, name):
# red = inputImage[:1024]
# green = inputImage[1024:2048]
# blue = inputImage[2048:]
# formatted = np.zeros([3,32,32])
# formatted[0] = np.reshape(red,[32,32])
# formatted[1] = np.reshape(green,[32,32])
# formatted[2] = np.reshape(blue,[32,32])
# final = np.swapaxes(formatted,0,2)/255
final = inputImage
final = np.rot90(np.rot90(np.rot90(final)))
imsave(name, final)
def main(argv=None):
display()
# train()
if __name__ == '__main__':
tf.app.run()
| [1] | http://caffe.berkeleyvision.org/ |
| [2] | http://cs224d.stanford.edu/ |
| [3] | https://www.udacity.com/course/deep-learning–ud730 |
| [4] | http://www.deeplearningbook.org/ |
| [5] | https://plus.google.com/+YoshuaBengio/posts |
| [6] | https://www.quora.com/session/Andrew-Ng/1 |
| [7] | https://www.facebook.com/yann.lecun?fref=ts |
| [8] | (1, 2, 3) https://plus.google.com/111541909707081118542/posts/P8bZBNpg84Z |
| [9] | http://www.johnloomis.org/ece563/notes/filter/conv/convolution.html |
| [10] | http://neuralnetworksanddeeplearning.com/chap2.html |
| [11] | https://en.wikipedia.org/wiki/Rectifier_(neural_networks) |
| [12] | https://grzegorzgwardys.wordpress.com/2016/04/22/8/#unique-identifier |
| [13] | http://neuralnetworksanddeeplearning.com/chap2.html#the_backpropagation_algorithm |
| [14] | (1, 2) Zeiler, Matthew D., and Rob Fergus. “Visualizing and understanding convolutional networks.” European conference on computer vision. Springer International Publishing, 2014. |